ResLibCal: a tool to compute triple-axis neutron spectrometer resolution

1. Purpose
2. Obtaining the package
3. Installation - starting
4. Available computational methods
5. Usage to compute the TAS resolution function (with plots)
   1. ResLibCal: the main interface
   2. ResCal standard nomenclature for configurations
   3. The lattice and spectrometer coordinate frames
   4. Plotting the TAS resolution function
   5. Handling computation along a scan (measurement sequences)
   6. Loading previous configurations
   7. Exporting the results, saving the configuration
   8. Non interactive mode (compute only)
6. Convolution of the TAS resolution function with a model, in 4D
   1. Dispersion model: 4D dynamic structure factors S(q,w)
   2. Planned in the future
7. Help
8. Credits and disclaimer

Purpose

• ResLib (A. Zheludev)
• ResCal5 (A. Tennant and D. Mc Morrow)
• Res3ax (J. Ollivier)
• ResCal from (Hargreave,Hullah,1979), ported into vTAS_view (Y.Raoul/A. Bouvet/A. Filhol) [Fortran code]
• McStas (K. Nielsen, K. Lefmann, E. Farhi, P. Willendrup et al.) using the templateTAS (E. Farhi) instrument
  

Obtaining the package

Source code
The package can be obtained here [ZIP 220 ko]. You can also browse the source code here or get a copy.
It does not depend on any other toolbox/library, except Matlab. Simply extract the application archive.
In addition, the legacy RESCAL code is also made available as [Fortran code].

Binary pre-compiled (no need for Matlab)
It comes pre-installed in the iFit standalone distribution.

Installation - starting

>> ResLibCal;

>> addpath(genpath('/path/to/ResLibCal'))

% ifit ResLibCal

>> ResLibCal

Available computational methods

The Cooper-Nathans [1] method handles a conventional description of the instrument, with collimations and homogeneous mosaic spread.
The Popovici method [3] handles similarly collimations and mosaic spreads (but here with separate horizontal and vertical components), but also much more geometrical details, including the optical elements size, and the radius of curvature of the monochromator and analyzer. Modern TAS machines mostly use optics focusing so that this method is probably more suited to model today's spectrometers.
The Full Monte-Carlo uses a Monte-Carlo instrument simulation with McStas (templateTAS instrument) to evaluate the resolution as a cloud of points in the reciprocal space. This cloud can then be used for 4D convolution.

• the G matrix contains the horizontal and vertical collimation (alpha and beta parameters)
• the F matrix contains the monochromator and analyser mosaicity (vertical and horizontal)
• the A matrix holds the k_i³ cotan(θ_M) and k_f³ cotan(θ_A) resolution volume terms (apparent monochromator and analyzer beam cross sections)
• the B matrix represents the orientation of the sample (angle A3), i.e. the momentum exchange Q in the k_i frame
• the C matrix is roughly 1/2, with monochromator and analyzer projection terms.

• Cooper-Nathans/AFILL: the original Cooper-Nathans [1] code RESCAL from Brookhaven 'AFILL'. Mosaicities are isotropic (horizontal equals vertical). [Fortran code].
• Cooper-Nathans/ResCal5: a simple re-write of the Cooper-Nathans method [1] from the ResCal5 Matlab application. Mosaicities are isotropic (horizontal equals vertical).
• Cooper-Nathans/Res3: simple Cooper-Nathans based on notes from B. Hennion in the Popovici formalism [3], with correction [7].
• Cooper-Nathans/ResLib: an enhanced version of the Cooper-Nathans method [3] from the ResLib Matlab application, in the Popovici formalism [3]. The analyzer reflectivity is taken into account (with analyzer thickness 'WA'). Supports vertical and horizontal mosaic spreads, with correction [7].
• Popovici/ResLib: the Popovici formulation of the resolution [3]. The analyzer reflectivity is also taken into account (with analyzer thickness 'WA') and correction [7].
• Popovici/ResCal5: the Popovici formulation of the resolution [3], with vertical sample mosaicity , but homogeneous mosaicity for monochromator and analyzer [7].
• Full Monte-Carlo (McStas): the instrument is modeled as a source, a monochromator, a sample, an analyzer and a detector. The simulation is assembled using McStas [8] and compiled locally from a C source. This is the most accurate description of the instrument.

The Cooper-Nathans/AFILL method uses the Chesser and Axe intensity estimate [2], whereas all the other methods use the Popovici formulation [3]. The intensity estimate is given w.r.t the source, and is given in [a.u.]. The monochromator and analyzer reflectivity is assumed to be ideal (1).
The intensity with the Full Monte-Carlo model provides the best estimate.

In all methods, the alpha/beta collimation parameters support guide m-coating specification (negative values e.g. -2) which are then converted to equivalent critical angles 0.1 m λ_i [deg]. The alpha/beta collimations are also limited by the effective divergence set from the geometry, e.g. atan(width or height/distance) [rad].
The collimations with the Full Monte-Carlo model provides the best estimate, as they are indeed modeled as Soller type collimators.

The sample mosaic spread is also taken into account, as well as a correction for the sample orientation w.r.t. the incoming beam.
In the legacy Cooper-Nathans formalism, all mosaic spreads are isotropic (monochromator, analyzer, sample). In the Cooper-Nathans/Popovici formalism, mosaicity supports separate vertical and horizontal components, including correction [7].
In the Popovici formalism, all mosaicities are taken into account with separate vertical and horizontal components (monochromator, analyzer, sample).
The mosaicities with the Full Monte-Carlo model are assumed with a gaussian reflectivity profile.

Usage to compute the TAS resolution function (with plots)

• The File menu allows to import a saved configuration, export the main window image, print it, reset to the default/saved configuration, and quit.
• The View menu allows to select the representation of the resolution matrix, as 2D or 3D view, select if you wish to compute it in the lattice frame (rlu), show the vertical Qz component or the energy, or in the instrument frame (Q axis), force a re-computation manually, or allow an automatic re-computation of the resolution when any change is made in the GUI.
• The Help menu mainly bring you here.
  

ResLibCal: the main interface

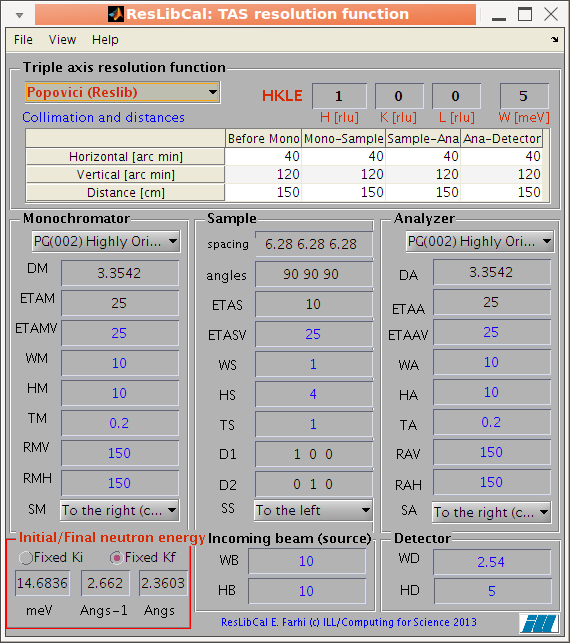
The main interface present all parameters required to configure a Cooper-Nathans or Popovici computation. All items have a contextual help (bring the mouse pointer over to display a short tool-tip, with signification and units). Parameters indicated in blue are used only in for the Popovici method. Parameters in red are those which the user should mostly change (incident energy, position of measurement HKLE) once the instrument configuration has been set.

The Q and Energy transfer are defined as:

The main parameter categories are:

• The method to use (Popovici is usually a good choice as a start)
  
• The HKLE position, which can be vectors for computations along a scan/set of positions
• The collimators and distances in a table
• The monochromator configuration
• The sample configuration
• The analyzer configuration
• The incident beam and detector sizes
• The neutron energy setting

When any value is changed, an automatic re-computation is performed if the View/Auto-update menu item is checked (which is the default).
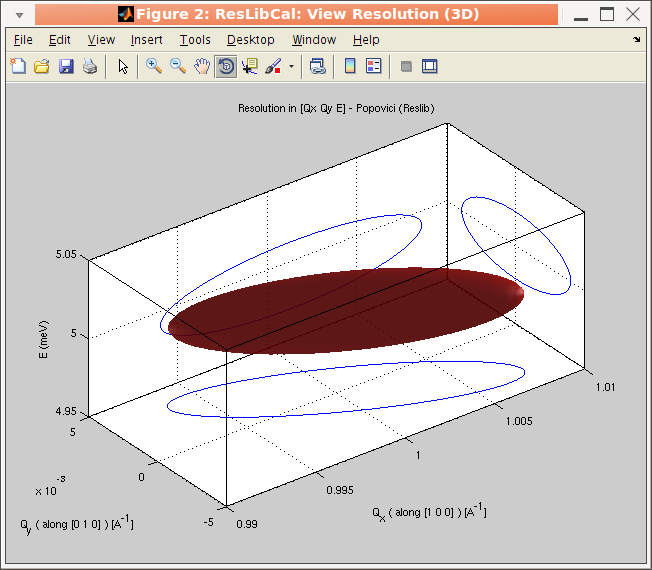
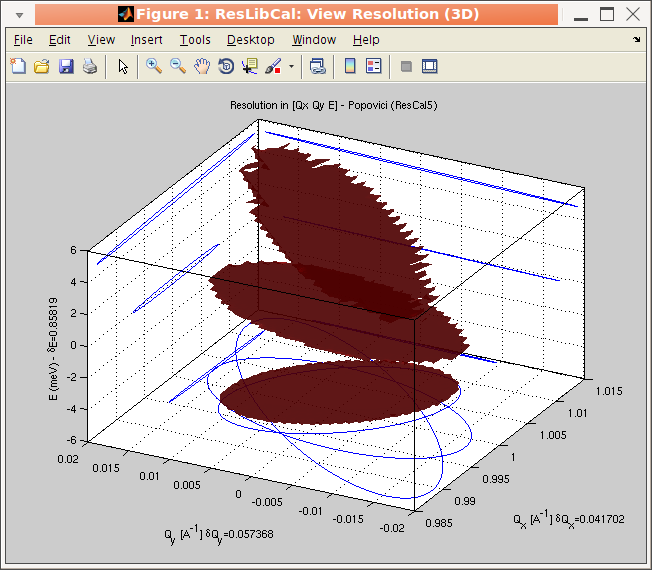
The result of the computation can be displayed from the View menu in 2D and 3D, as well as the instrument geometry.

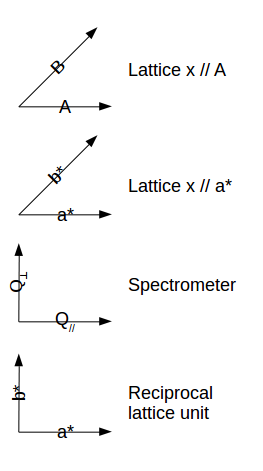
The resolution matrix is then shown in reciprocal lattice units (rlu) [a*,b*,E] or inverse Angstroem (Angs^-1) [Qx,Qy,E or A,B,E] . You can select the coordinate frame used for displaying the resolution in the Un-checking the Resolution in ... sub-menu in the View menu. See below for a description of the available coordinate frames. It is also possible to plot the resolution function projections in the vertical [Qz, c* or C]  axis instead of the energy E axis by toggling the View menu, e.g. Resolution in [Qx,Qy,E] item.
The resolution matrix is always computed in [Angs^-3.meV], but it can be shown in [rlu³.meV] in the 2D and 3D views.

The ResLibCal main interface. All items have contextual help. When the View/Auto-update menu item is checked, any change in the interface triggers a re-computation of the resolution, and an update of opened plots.

The collimations are given in [arcmin], but are bound between 0 and the geometrical angular aperture defined by the distances and dimensions of the spectrometer parts. The source-monochromator collimations (ALF1 and BET1) can be defined as a wavelength dependent divergence when given a negative value '-m' for a guide m-coating reading: 0.1 m λ_i [deg] where λ_i is the incident wavelength.

The monochromator and analyser curvatures can be given as the curvature radius [in cm], or set to 0 for a flat geometry, or to a negative value (e.g. -1) to request an automatic computation using the following expressions (for both monochromator and analyser):

RV = 2*L*sin(θ)
RH = 2*L/sin(θ)

where θ is the tilt angle, and 1/L=1/L_before + 1/L_after is the effective focal distance.

ResCal standard nomenclature for configurations

The user interface and configuration files lists parameters with the legacy ResCal naming. The meaning of the configuration parameters is the following

DM Monochromator d-spacing
DA Analyzer d-spacing
ETAM Monochromator mosaic
ETAA Analyzer mosaic
ETAS Sample mosaic
SM scattering sense frocdm monochromator +1=right, -1=left
SS scattering sense from sample +1=right, -1=left
SA scattering sense from analyzer +1=right, -1=left
KFIX fixed neutron wavevector in Ang.-1
FX index for fixed wavevector 1=incident 2=final (10)
ALF1 horizontal source-mono. collimation in min (FWHM)
ALF2 horizontal mono.-sample collimation in min (FWHM)
ALF3 horizontal sample-analyser collimation in min (FWHM)
ALF4 horizontal analyser-detector collimation in min (FWHM)
BET1 vertical source-mono.  collimation in min (FWHM)
BET2 vertical mono.-sample collimation in min (FWHM)
BET3 vertical sample-analyser collimation in min (FWHM)
BET4 vertical analyser-detector collimation in min (FWHM)
AS sample lattice parameter a in Angs.
BS sample lattice parameter b in Angs.
CS sample lattice parameter c in Angs.
AA (alpha) angle in deg. between axes b and c
BB (beta)  angle in deg. between axes a and c
CC (gamma) angle in deg. between axes a and b
AX First wavevector in scattering plane coordinate H (rlu). angle <KI,A>=A3
AY First wavevector in scattering plane coordinate K (rlu)
AZ First wavevector in scattering plane coordinate L (rlu)
BX Second wavevector in scattering plane coordinate H (rlu)
BY Second wavevector in scattering plane coordinate K (rlu)
BZ Second wavevector inou scattering plane coordinate L (rlu)
QH Position of resolution wavevector (center of measurement) H (rlu)
QK Position of resolution wavevector (center of measurement) K (rlu)
QL Position of resolution wavevector (center of measurement) L (rlu)
EN (W) Position of resolution wavevector (center of measurement) W (meV)
DQH Increment of Q,E defining general scan step along QH (rlu)
DQK Increment of Q,E defining general scan step along QK (rlu)
DQL Increment of Q,E defining general scan step along QL (rlu)
DEN Increment of Q,E defining general scan step along EN (meV)
GH Gradient of the dispersion (planar) direction along QH (rlu)
GK Gradient of the dispersion (planar) direction along QK (rlu)
GL Gradient of the dispersion (planar) direction along QL (rlu)
GMOD  Gradient of the dispersion (planar) direction along EN (meV)
BeamShape =0 for circular source, =1 for rectangular source
WB width/diameter of the source (cm)
HB height/diameter of the source (cm)
Guide =0 No Guide, =1 for Guide
GDH horizontal guide divergence (minutes/Angs)
GDV vertical guide divergence (minutes/Angs)
SampleShape =0 for cylindrical sample, =1 for cuboid sample
WS sample width/diameter perp. to Q (cm)
TS sample width/diameter along Q (cm)
HS sample height (cm) (10)
DetectorShape =0 for circular detector, =1 for rectangular detector
WD width/diameter of the detector (cm)
HD height/diameter of the detector (cm)
TM thickness of monochromator (cm)
WM width of monochromator (cm)
HM height of monochromator (cm)
TA thickness of analyser (cm)
WA width of analyser (cm)
HA height of analyser (cm)
L1 distance between source and monochromator (cm)
L2 distance between monochromator and sample (cm)
L3 distance between sample and analyser (cm)
L4 distance between analyser and detector (cm)
RMH horizontal radius of curvature of monochromator (cm)
RMV vertical radius of curvature of monochromator (cm)
RAH horizontal radius of curvature of analyser (cm)
RAV vertical radius of curvature of analyser (cm)

The lattice and spectrometer coordinate frames

The resolution can be obtained and displayed in 2 coordinate frames:

• Lattice / User [x // A, ABC] is relative to the user-defined A and B vectors which define the scattering plane ([U] matrix). These vectors are specified in rlu from the main interface. The vector A is normalised [to get Angs^-1], the vector B is used to compute a 'vertical' axis C = A x B, and then a vector B' is computed so that the ABC frame is ortho-normal, with x // A and 'C' vertical. The angle A3=<Ki,A>. This is the default frame.
• Lattice [x // a*, a* b* c* cartesian] is relative to the sample lattice Cartesian  frame ([B] matrix). The coordinate frame is defined by the a*, and two vector b'* and c'* forming an ortho-normal frame. The resolution is given in [Angs^-1.meV]. This is a convenient frame to visualise the reciprocal lattice, independently of the sample orientation in the spectrometer.
• Spectrometer [spec] is relative to Q, and vertical axis (spectrometer frame) ([Q] matrix). The [spec] coordinate frame is direct ortho-normal (cartesian), with x // Q and z vertical. The corresponding resolution matrix is 'spec.RM' given in [Angs^-3.meV]. It is especially suitable for powders and liquids.
• Reciprocal lattice unit [rlu] is relative to the sample lattice frame ([a*b*c*] matrix). The coordinate frame is defined by the a*, b* and c* lattice vectors, as specified by the AS,BS,CS lattice parameters, and angles AA,BB,CC (aka α, β, γ). The corresponding resolution matrix is 'rlu.RM', given in [rlu³.meV]. WARNING: in this frame, all lattices appear ortho-normal, as we use a*, b* and c* as axes, and plots use a Cartesian frame for rendering, even when e.g. γ=120.

The usual definition of the sample reciprocal lattice orientation vectors A and B (defined by the user), are so that the spectrometer angle A3 is the angle between KI and A=(AX,AY,AZ). The B=(BX,BY,BZ) vector defines a second lattice vector in the scattering plane. This is why, in order to properly define the [A,B] basis, an initial measurement is done in practice on a Bragg signal with Q=[QH,QK,QL]=[AX,AY,AZ]. For such a measurement, the [rlu] and [spec] frames are equivalent in a cubic lattice. Then the A3 angle offset is set to the signal maximum.

Plotting the TAS resolution function

The 2D plot of the TAS resolution function, with a text box containing the computation results and detailed configuration.

The 3D plot of the TAS resolution function. The axis has a contextual menu allowing to change the plot rendering.

A geometric representation of the TAS can be shown in real space, using the instrument configuration parameters. This view is generated from the View/Instrument geometry menu item. It is automatically updated upon change of instrument parameters, as the other views.
The signification of the angles shown is as follows:

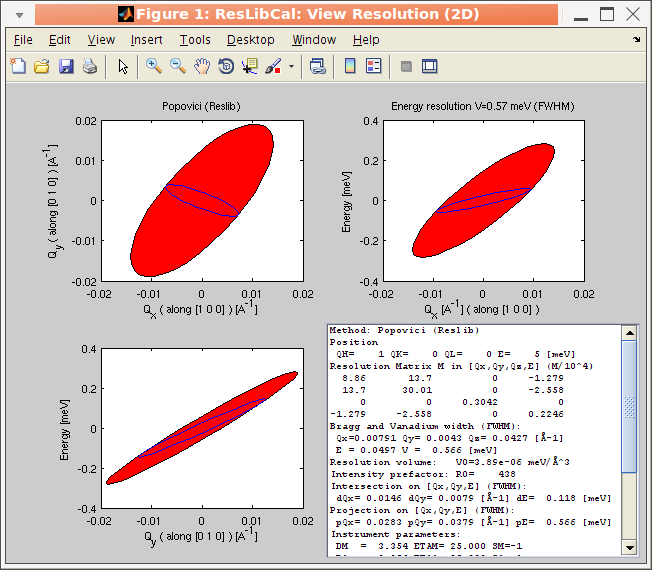
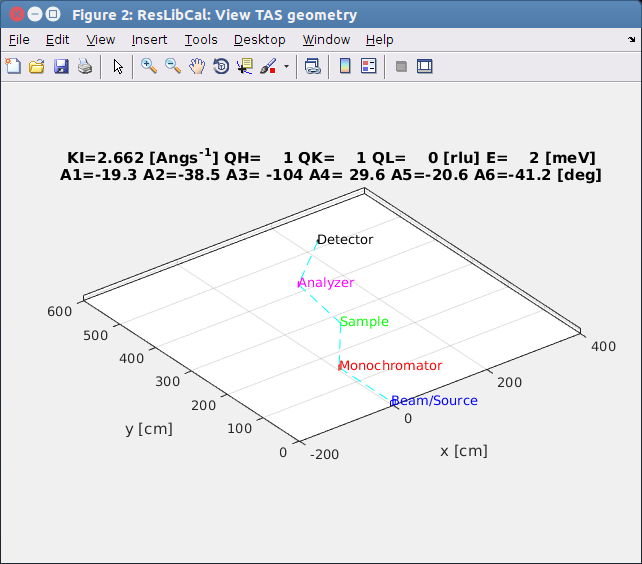
A1  rotation angle of the monochromator. A1=0 means the crystal is in grazing incidence.
A2  scattering angle (take-off) from the monochromator, usually A2=2*A1 in scattering condition.
A3  orientation angle of the crystal lattice in real space. This is the angle between KI and vector A=(AX,AY,AZ)
A4  scattering angle (take-off) from the sample. Usually A4 is NOT 2*A3.
A5  rotation angle of the analyser. A5=0 means the crystal is in grazing incidence.
A6  scattering angle (take-off) from the analyser, usually A6=2*A5 in scattering condition.
 

The 3D plot of the TAS geometry. The axis has a contextual menu allowing to change the plot rendering.

Last, it is possible to generate a full report with all views and configuration parameters as an HTML document via the File:Print menu item, or the Save as... HTML document.

Handling computation along a scan (measurement sequences)

Any HKLE setting can be assign a vector, so that the resolution will be computed, and plotted in GUI mode for all measurements. The vector should be set as values separated by spaces.
An example is for instance

H=1 K=0 L=0
W=-5 0 5

which shows a 3 steps scan along the energy axis.

Loading previous configurations

The 'File/Open...' menu item allows to read a saved ResLibCal configuration (*.m, *.ini, see below), a ResCal5 configuration (*.par, *.cfg, 42 or 27 numbers), or any file with named Rescal parameters, such as in an ILL TAS data ascii file and from ResTrax (*.res). SPEC (AFIT) files from LLB can also be read (do not contain sample information).

Getting configuration from other packages:
The *.res files can be generated by ResTrax. This is a list of NAME=VALUE pairs.
The *.par and *.cfg files can be generated by ResCal5.
The *.par files can be generated by the legacy ResCal code (42 values in a column).
ResTrax can also generate *.cfg files (different format than ResCal5), which only specify a reduced set of parameters (we refer to these as 'rtx' files when exporting to avoid confusion).

In addition, the 'File/Open Instrument...' menu item allows to read a predefined TAS instrument configuration. These instruments are stored in the ResLibCal/instruments directory. Such files should preferably be '.ini' files, but any other supported configuration format also works. We currently provide such files for IN1 IN8 IN14 IN20 IN22  MLZ_TRISP. You may add files in this location with your preferred configurations by just copying and renaming e.g. any ResLibCal.ini file.

Exporting the results, saving the configuration

Rescal legacy format (*.dat):
If the output file name you specify has a 'dat' extension, the generated configuration uses the ResCal legacy format, which consists in 42 numbers.

Rescal legacy format (*.par and *.cfg) with comments:
If the output file name you specify has a 'par' or 'cfg' extension, the generated configuration uses the ResCal legacy format, which consists in 42 numbers. Comments are added for easier parameter identification. An additional cfg file with Popovici parameters will also be written. These files can be read by the legacy ResCal and ResCal5.

ResTrax/ResCal format (*.res):
If the output file name you specify has a 'res' extension, the generated configuration uses a simple 'NAME = value' list of parameters. Such files can be read by ResTrax.

ResTrax legacy format (*.rtx):
If the output file name you specify has a 'rtx' extension, the generated configuration uses the ResTrax legacy format. This type of file only exports a reduced number of parameters.

HTML report (*.html)
Save the whole configuration and results, including the  2D/3D/geometry views, into an HTML document.

Non interactive mode (compute only)

>> out = ResLibCal('config_file')
ans =
         Title: 'ResLibCal configuration'
        handle: 173.0160
           EXP: [1x1 struct]
    resolution: [1x1 struct]
        ResCal: [1x1 struct]

>> out = ResLibCal('DA=3.355; DM=3.355; ...')	% change the configuration and recompute resolution

>> out = ResLibCal(out or EXP structure, 'DA=3.355; DM=3.355; ...')
>> out = ResLibCal(out or EXP structure, 'file')

>> out = ResLibCal(2,0,0,5) 	% computes at HKLE=[2 0 0 5] coordinates in r.l.u
>> out = ResLibCal('QH=2 W=5')  % same as above but giving configuration as a string with named parameters

>> out.resolution
     focus: [80.0088 439.4046 49.7513 136.3181]
        R0: 16.5334		% the intensity
      HKLE: [2 1 0 5]		% the HKLE rlu.meV coordinate of this point
    method: 'Popovici (ResLib)'
    README: {2x1 cell}
      spec: [1x1 struct]	% spectrometer frame
       rlu: [1x1 struct]	% lattice frame [a*, b*, c*]
      cart: [1x1 struct]
   rlu_ABC: [1x1 struct]
       ABC: [1x1 struct]
    angles: [25.2592 50.5184 14.3768 -70.9737 37.1658 74.3316]	% A1-6 angles in a TAS machine
         Q: 2.2361

>> out.resolution.rlu
    cart2frame: [3x3 double]
     rlu2frame: [3x3 double]
             Q: [3x1 double]
            RM: [4x4 double]
        README: '[R] rlu lattice frame, xyz=[a* b* c*]'
          unit: 'rlu'
         frame: [3x3 double]
     frameUnit: '1/\C5'
      frameStr: {1x3 cell}
         Bragg: [5x1 double]
         cloud: {[2000x1 double]  [2000x1 double]  [2000x1 double]  [2000x1 double]}

>> out.ResCal
ans = 

                DM: 3.3542
                DA: 3.3542
              ETAM: 30
              ETAA: 25
              ETAS: 5
                SM: -1
                SS: 1
                SA: -1
              KFIX: 2.6620
                FX: 2
              ALF1: 40
              ALF2: 40
              ALF3: 40
              ALF4: 40
              BET1: 120
              BET2: 159.9648
              BET3: 120
              BET4: 120
                AS: 6.2800
                BS: 6.2800
                CS: 6.2800
                AA: 90
                BB: 90
                CC: 90
                : 1
                AY: 0
                AZ: 0
                BX: 0
                BY: 1
                BZ: 0
                QH: 2
                QK: 0
                QL: 0
                EN: 0
               DQH: 0
               DQK: 0
               DQL: 0
               DEN: 1
                GH: 0
                GK: 0
                GL: 1
              GMOD: 0
         BeamShape: 1
                WB: 10
                HB: 10
             Guide: 0
               GDH: 0
               GDV: 0
       SampleShape: 1
                WS: 1
                TS: 1
                HS: 4
    DetectorShape: 1
                WD: 2.5400
                HD: 5
                TM: 0.2000
                WM: 10
                HM: 10
                TA: 0.2000
                WA: 10
                HA: 10
                L1: 150
                L2: 150
                L3: 150
                L4: 150
               RMH: 0.0067
               RMV: 0.0067
               RAH: 0.0067
               RAV: 0.0067

>> out=ResLibCal;	% contains the ResLib structure as out.EXP
>> out.EXP.method = 'Cooper-Nathans ResCal'

>> [ out.EXP.QH out.EXP.QK out.EXP.QL out.EXP.W ]
ans =
     2     0     0     0
>> out.EXP.W = 1;		% change the position in reciprocal space
>> out = ResLibCal(out);	% request a new computation with modified choices

Convolution of the TAS resolution function with a model, in 4D

1. compute the resolution function
2. build a Monte-Carlo cloud of points which is a random statistical description of the TAS response
3. evaluate the dispersion for all points in the resolution cloud, and sum it to get an estimate of the integrated counts on the detector arising from the 'capture' of the dispersion by the TAS resolution function.

>> s_tas = conv(s, 'tas')
>> s_tas = ResLibCal(s);

>> d_4d = ResLibCal(d);

Dispersion model: 4D dynamic structure factors S(q,w)

S(q,w)	Description	Dimensionality	Parameters
sqw_sine3d	Phonon dispersions as sine wave in HKL (3D) with a damped harmonic oscillator energy dispersion	4D (HKLw)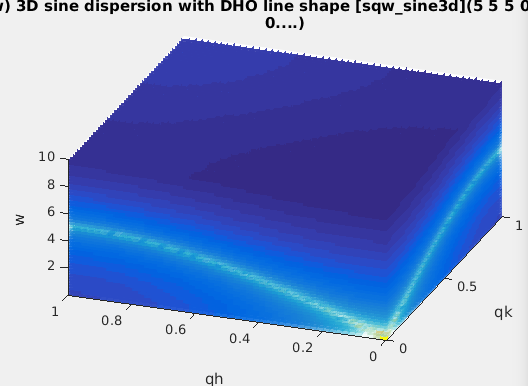	zone center, energy gaps, periodicity
sqw_vaks	Phonon dispersions in perovskite cubic crystals using the Vaks parameterisation	4D (HKLw)	acoustic and optical , coupling parameters, soft mode frequency
sqw_cubic_monoatomic	Phonon dispersions in a monoatomic cubic crystal using the Dynamical matrix.	4D (HKLw)	acoustic force constant ratio and scaling energy
sqw_phonons	Phonon dispersions from the Dynamical matrix, using forces estimated by ab-initio usingASE and a selection of DFT codes (EMT, GPAW, ABINIT, Elk, Dacapo, NWChem, QuantumEspresso, VASP).	4D (HKLw)	Creation: POSCAR, CIF, or PDB, ... Then, only the DHO line shape. ab-initio implies no (few) tunable parameter.
sqw_spinw	Spin-wave dispersion in HKL using SpinW. Ann initial SpinW object must be given, or defaults to the 'squareAF' with J1=2, J2=0	4D (HKLw)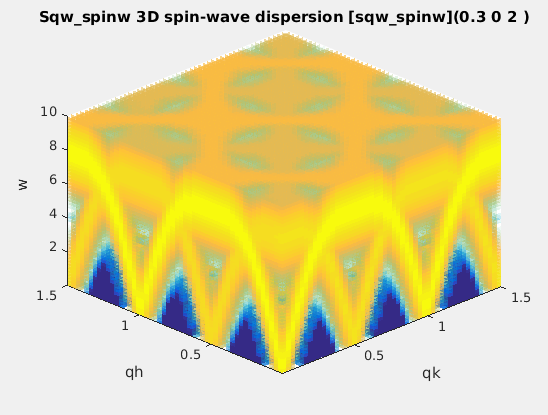	energy broadening, Temperature, Amplitude, coupling parameters J...
sqw_linquad	A phenomenological dispersion which can describe an acoustic or optical mode. This model can be considered as a local expansion in series of any dispersion.	4D (HKLw)	Energy and location of 'gap', slopes, directions of slopes, DHO width, temperature, background
sqw_acoustopt	A phenomenological dispersion which can describe an acoustic or optical mode.Acoustic slope and 'optical' minimum energy can be specified.	4D (HKLw)	Energy and location of 'gap', slopes, directions of slopes, DHO width, temperature, background

    s=sqw_sine3d; % create a 4D S(q,w) for a cubic pure material, using default parameters
    t=ResLibCal(s);         % convolute it with a TAS resolution, and open ResLibCal.

    w=linspace(0.01,10,50); qh=1.1*ones(size(w)); qk=0*qh; ql=0*qh; % an E-scan around the [1 0 0] Bragg
    signal0=iData(s, [], qh,qk,ql,w);	% the ideal model evaluated along the HKLE line
    signal1=iData(t, [], qh,qk,ql,w);   % the convoluted model evaluated along the HKLE line

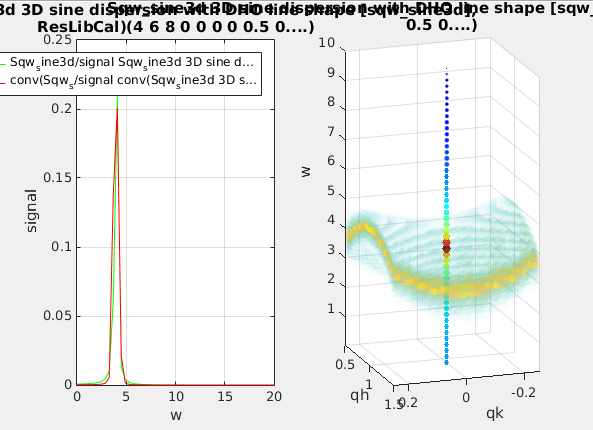
    figure; plot(squeeze([signal0 signal1/100])); % plot the dispersion and simulated measurement

    QH=linspace(0,1.5,50); QK=linspace(-.25,.25,50);; QL=QK; W=linspace(0.01,10,51);	% a 4D grid
    f=iData(s,[],QH,QK,QL,W);						% evaluate the model on the 4D grid
    figure; plot3(log(f(:,:,25,:)));  					% plot dispersion
    hold on; scatter3(log(signal1(:,:,1,:)),'filled');			% overlay the simulated scan

Planned in the future

• Support polarisation analysis in the models.
  
• Support PhonoPy FORCE_SET input and PHONON/VASP HFFILE.
• Provide more S(q,w) phonons with the small displacement method (ASE, LJ, Morse, LAMMPS, VASP, GPAW, AbInit). Not done, but can be improved in ASE.
  
• Provide more S(q,w) models, e.g. molecular dynamics trajectories (ASE, NAMD, Moldy, GROMACS, ...), using nMoldyn/MDANSE for FFT.
• Handle S(|q|,w) 2D dispersions for e.g. powders, liquids, disordered systems.
• Provide 2D S(|q|,w) models from e.g. NJOY/LEAPR.
• Properly handle mode polarisation and line-width/amplitude per branch in supplied models. Properly evaluate mode intensity. Now done in sqw_phonons.
• Extend the methodology to diffraction and time-of-flight neutron scattering instruments.
• Faster 4D convolution using Gaussian integrals.
• Integrate S(q,w) for spin-waves from SpinW. Now done, but would require a better model editor.
  
• Couple with Horace. Now partly done.
  
• Support the resolution function/matrix estimate from McStas and ResTrax.

Help

1. your Matlab version
2. the ResLibCal version which you can get from the Help/About menu item.
   
3. the TAS configuration you use and the associated procedure to reproduce the error
   
4. a copy of the error messages produced by the script/command.
   
5. a smile ;-)

Credits and disclaimer

• ResLib (A. Zheludev), using especially ResMat, ResMatS and ResPlot3D
• ResCal5 (A. Tennant and D. Mc Morrow), using especially rc_cnmat, rc_popma, rc_projs
• Res3ax (J. Ollivier), using res35
• ResCal from (Hargreave,Hullah,1979), ported into vTAS_view (Y. Raoul/A. Bouvet/A. Filhol) and PKFit. [Fortran code]
• McStas (K. Nielsen, K. Lefmann, E. Farhi, P. Willendrup et al.) using the templateTAS (E. Farhi) instrument

E. Farhi, Y. Debab and P. Willendrup, J. Neut. Res., 17 (2013) 5. DOI: 10.3233/JNR-130001

 E. Farhi - ResLibCal - Aug. 22, 2017 1.10