iFit: iFunc object description


Commands we use in this page: iFunc, save(iFunc, filename), fits
See also: iData, Load (import) data sets, Low level Loaders, Save (export) data sets

The iFunc class is a structure which holds a multi-parameter model, to be used for e.g. plot or fit onto a data set. Models can be assembled using standard Matlab operators. There exist a set of pre-defined Models, which you can assemble to define more complex ones. You can also Fit an iFunc model onto an iData object (containing e.g. some experimental data).

The iFunc Models also exist in a set of specialized flavours (sub-classes) which inherit full iFunc capabilities, and add a few more specialized functionalities:

Creating and inquiring iFunc models (iFunc, get, plot, subplot)

A model object holds an Expression (to compute the model value), a list of parameter names, a Guess expression to compute parameter value estimates, as well as other MetaData just as for iData objects.

To create a model (i.e. instantiate a class into an object), specify its Expression, using
For instance a linear model is obtained with
>> a=iFunc('p(1)*x+p(2)')

a =  iFunc 1D model:

    [Tag] [Dim]                                [Model] [Parameters 'p']
 iF193482   1        p(1)*x+p(2)  signal = p(1)*x+p(.. Amplitude Constant 

>> a=iFunc('a=p(1); b=p(2); signal=a*x+b');	% same as above
Any expression can be entered, and an analysis of the parameters results in default parameter names.

You can then display the full content of the object with the disp or get methods :
>> disp(a)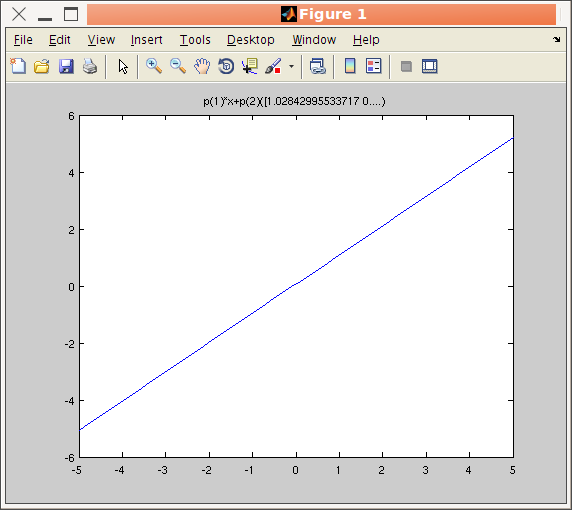iFunc: plot
a = iFunc 1D model:
         Expression: signal = p(1)*x+p(2);
                Tag: 'iF193482'
               Date: '17-Jul-2012 10:49:50'
               Name: ' p(1)*x+p(2)'
         Parameters: {'Amplitude'  'Constant'}
          Dimension: 1
    ParameterValues: []
           UserData: ''

Parameters:
  p(  1)=           Amplitude
  p(  2)=            Constant

>> plot(a)
A graphical representation of the model is obtained using the plot method.

Properties of the model can be obtained with the get method, or with direct indexing :
>> get(a, 'Expression')
>> a.Expression
ans =

signal = p(1)*x+p(2);
The Expression can be a character string returning the 'signal' as a function of the parameters 'p' and axes x,y,z,t,u,v,w
It can also be given as a function handle signal=@Expression(p, x,y, ...), which usually makes the model evaluation much faster.
>> a=iFunc(@(p,x)p(1)*x+p(2))
Additional arguments (above the model dimensionality) are usable in the Expression as 'varargin' cell.
The name of the parameters can be changed by accessing the Parameters property (this is a cell of strings) :
>> a.Parameters = {'Slope','Constant'}
The ParameterValues property holds the last parameter values (e.g. when returned from a fit or a function evaluation).
The Guess property should return a vector of parameter values 'p' as a function of the axes x,y,z... and a signal. This is a character string, vector or a function handle p=@Guess(x,y,z, ..., signal). Values of the parameters left as NaN indicate that the automatic guess procedure should be used (which is based upon a signal peak search, and baseline analysis). The Guess is used when starting a fit procedure for starting parameters.
Last, the Constraint property holds any script to change the parameter values (character string modifying 'p') from axes x,y,z,... or a function handle p=@Constraint(p, x,y,...). See below on how to define Constraints.

The model dimension, i.e. the number of axes required for its evaluation, is stored in the Dimension property. 0=scalar, 1,2,3,4 ...
A negative dimension is used to indicate a variable dimensionality, i.e. the model can accept more axes, or dimensionality is defined after instantiation.

To print out the equivalent function f(p, x, ...) from an object, convert it to a char or cellstr:
>> a=iFunc('p(1)*x+p(2)')
>> char(a)
>> cellstr(a)
Last, it is possible to define an empty iFunc object, and fill it with Parameters and any Expression, even without actually any mathematical model:
>> a=iFunc;
>> a.Parameters={'Amplitude','Width'}
>> a.Expression=[ '[ varargin{:} ]' ];
This way, it is possible to define any Matlab function inside an iFunc object. The cell 'varargin' then contains the arguments 2-end, while 'p' contains the first argument.
>> a(1,2,3)
ans =
     2     3

Accessing or modifying parameter values

Parameters from a model can be accessed in many equivalent ways. If 'a' is an iFunc model :

>> a.Parameters		% lists all parameter names
>> get(a)		% display the model description, with the list of parameter names and last evaluated values
>> a.p			% returns a vector of parameter values
>> a.ParameterValues	% same as above, last evaluated parameter values

If, for instance, the model has an 'Slope' parameter, you can get specifically its value with :

>> a.Slope		% display the value of the 'Slope' parameter

Alternatively, it is possible to modify parameter values :

>> a.p(1) = 2;
>> a.Slope = 2;

Defining a new model

To define a new model with a dialogue window, use:
>> edit(iFunc)
iFunc: subplotRefer to the dedicated help on this topic in the Models page, which also lists pre-defined models (Gaussian, Lorentzian, exponential, lines, quadratic, ...). Edit their code to see how to define new models:
>> edit gauss % edit the function definition (from a file)
>> edit voigt
>> edit(voig) % edit the object definition
When no parameter value is known, some guessed values are estimated from the analysis of the model value and expression.

The plot method demonstrated above can display a set of models in a single axis frame, or a set of panels (subplot) :
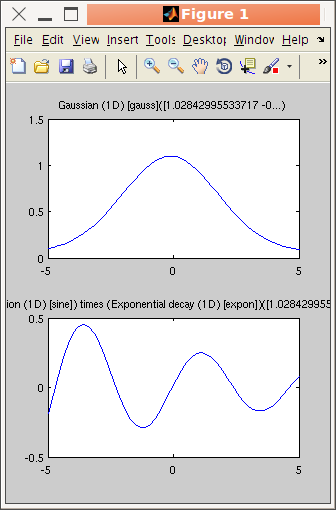
>> plot([gauss lorz])
>> subplot([gauss sine.*expon])	% use unary and binary operators, see below

Model from a tabulated data set

It is also possible to create a model out of an iData (data set) object. Then, the model parameters are the total intensity scaling, as well as an offset and a scaling factor per axis. In order to create a model from a data file, use:
	>> iFunc(iData('filename'))
will create a data set object and derive a model out of it.

Evaluating a model with parameter values and axes

The syntax for evaluating a model is


model(parameters)                            % use guessed axes

model(parameters, x,y, ...)                % use given axes

feval(model, parameters, x,y,z, ...)

iData(model, parameters, x,y,z, ...)    % evaluate and convert into an iData object

where parameters can be a numerical vector, or a structure with named parameters matching the model ones, x,y,z,t,u,v,w are axes values for ranks 1,2,3... Additional arguments (above the model dimensionality) are usable in the Expression as 'varargin' cell.

When the parameters are specified as empty ( [] ), current parameter values are used, or guessed. These parameters can also be given as a vector corresponding to the model parameter order, a string such as 'Intensity=1; Width=.5', a structure with named fields and values such as:
The evaluation of a model with a set of parameters is obtained by calling the feval function with the parameter values, or sending these values directly to the object :
>> signal = feval(gauss, [ 1 0 .1 0])
>> gauss([ 1 0 .1 0])			% same as above: evaluate model
In this case, tentative axes are computed from the model definition. Axes can also be passed as additional arguments for x,y,z,... either as separate arguments, as a cell array {x,y,...}, as a structure, or as an iData object which axes are used.
>> feval(gauss, [ 1 0 .1 0], linspace(-5,5, 100) )
>> gauss([ 1 0 .1 0], linspace(-5,5, 100) )		% same as above: evaluate model
When used together with iData objects, the iFunc models can either return their evaluation (array), or be converted into an iData object for easier further handling.
>> iD = iData(linspace(-5,5, 100), zeros(1,100));	% define a zero iData object with some axes
>> g  = gauss; 						% a Gaussian model
>> g([ 1 0 .1 0], iD)					% evaluate model with axes in the iData object
>> iD(g, [1 0 .1 0])					% evaluate model into a new iData object
A faster calling syntax for the same result is:
>> g=gauss;
>> iData(g, [1 0 .1 0], linspace(-5,5, 100), zeros(1,100))	% evaluate model into a new iData object
It is also possible to evaluate the model while scanning parameters. To achieve that, the parameter values must be given as a named structure, or as a string such as 'Intensity=[ .5 1 1.5 2 ];'

For instance, to scan the Intensity parameter in a Gaussian, and get the model value as an array of data sets, use:
Scans with multiple parameters vectors can be performed the same way.

Setting and removing constraints on models

Models are often used for fitting purposes (refer to the Fit help page).

To set a constraint on a model parameter, define the 'constraint' input argument when calling fits (see Fit) or set the constraint directly on the model parameters with:
>> model.parameter='fix'     % to lock its value during a fit process. Same as mlock
>> model.parameter='clear'   % or 'free' to unlock value during a fit process. Same as munlock
>> model.parameter=[min max] % to bound value
>> model.parameter=[min value max] % to bound the parameter and set its value
>> model.parameter=[nan nan] % to remove bound constraint
>> model.parameter=''        % to remove all constraints on 'parameter'
>> model.parameter='expression'        % to set the parameter from an expression which can use 'p(n)' for other parameters
>> model.Constraint=''       % to remove all constraints
>> model.Constraint = 0;     % to unlock/free all Parameters during a fit process
>> model.Constraint = 1;     % to lock/fix all Parameters during a fit process
Any parameter name surrounded by double quotes, e.g. "Amplitude", is replaced by the corresponding p(n) value in an expression used for setting a parameter value (cross-constraints). For instance
>> f=gauss;			% create a Gaussian model
>> f.Amplitude = 'fix';		% fix its Amplitude
>> f.Background = [0 1e-4];	% bound its background
>> f.Width = 'p(1)/1000';	% use an expression referring to p(1)=Amplitude value
>> f.Width = '"Amplitude"/1000';	% same as above with direct naming of parameters using ""
Alternatively, you can use the mlock, munlock and xlim methods:
>> mlock(f, {'Amplitude','Background'})	% fix these 2 parameters, same as setting parameters to 'fix' 
>> munlock(f, 'Background')		% unlock that parameter, same as f.Background='clear'
>> xlim(f,    'Background', [0 1e-3])	% force parameter within range, same as f.Background=[min max]
>> xlim(f,    'Background', [])		% remove limits constraint
Last, you can fix/clear/bound parameters based on a regular expression search such as:
>> mlock(f, regexp(f.Parameters, 'Amplitude|Background'})
where we have used the '|' OR operator.

To list parameters which are fixed, free and bound, use:
>> mlock(f)
>> munlock(f)
>> xlim(f)
which return the number of parameters in each category. This is also displayed when using:
>> disp(f)
Under the hood, the constraints are stored as a structure with fields min, max, fixed, set (with one expression per parameter), and eval (to be evaluated before the object Expression).

Saving objects for further re-use: save, saveas, load

Once you have created an manipulated a model, it is possible to export it into a file so that you can re-use it latter. To do so, use saveas(object, ...) similarly as when saving iData objects. 'save' is equivalent to saveas.

>> a=iFunc('p(1)*x+p(2)') + gauss ;
>> saveas(a);			% save as a Matlab m-file function, file name is automatically set to the model iD
>> saveas(a, '', 'mat')		% same, with a 'mat' file
>> save(a, 'model.mat')	% same, with a 'mat' file, specifying the file name

The supported export formats are [ as listed with saveas(iFunc,'formats') ]:

       DAT  Flat text file with comments (*.dat) 
       EPS  Encapsulated PostScript (color, *.eps) 
       FIG  Matlab figure (*.fig) 
   HDF4;H4  Hierarchical Data Format 4 image (*.hdf4) 
  HTML;HTM  Hypertext Markup Language document (*.html) 
       JPG  JPEG image (*.jpg) 
      JSON  JSON JavaScript Object Notation (*.json) 
         M  Matlab script/function (*.m) 
       MAT  Matlab binary file (*.mat) 
       PDF  Portable Document Format (*.pdf) 
       PNG  Portable Network Graphics image (*.png) 
        PS  PostScript (color, *.ps) 
  TIFF;TIF  TIFF image (*.tif) 
       XML  XML file (*.xml) 
  YAML;YML  YAML interchange format (*.yaml)

We recommend to save iFunc models as MAT files, or m-files or YAML.

To load back an m or mat file into memory for re-use:

Manipulating models: operators

Models can be assembled to create more complex models. This is achieved simply with unary and binary operators:

Unary operators
 abs char del2 floor sparse transpose  acos conj full sqrt uminus  acosh real  asin exp ndims round xcorr  asinh imag norm  atan cos isempty not sign tan  atanh cosh fliplr log sin tanh  ceil ctranspose flipud log10 plus(+) sinh minus(-)
Binary operators
 mtimes(*) times (.*) mpower(^) power(.^) mrdivide(/) rdivide(./) conv convn
Other operators
 edit plot char copyobj doc feval fits get set subplot conv convn xcorr save saveas

The full list of operators can be obtained from the 
>> methods iFunc
The element-wise times(.*), divide(./) and power(.^) operators apply the operation along the model dimensions, with parallel axes. 
The matrix-operators mtimes(*), 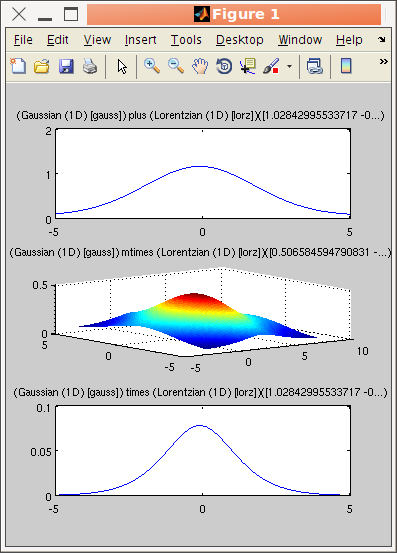iFunc: + .* and * operatorsmrdivide(/) and mpower(^) operator perform orthogonal axes multiplication, with extension of the model dimensionality.

Examples are easier to understand, so let's see a few operations :
>> a = gauss  + lorz;		% addition
>> b = gauss  * lorz; 		% orthogonal axes multiplication 2x 1D -> 2D
>> c = gauss .* lorz; 		% parallel axes multiplication
>> c.Constraint = 'p(8) = 0;';	% avoid having two Background parameters
>> subplot([a b c])
In binary operations, passing one of the arguments as a string will simply insert the corresponding code into the model Expression as the argument to the operator. For instance the following statement appends a zero value vector to the gauss model value (axes are x,y,z,... and parameters values are in p):
>> c = gauss + 'zeros(size(x))'
The addition operator plus (+) used with a string argument which contains an equal sign '=' or ';' character concatenates the string before/after the Expression of the model. For instance the following example does the same as above, explicitly setting the new signal value, and the next one displays a text before evaluating the model :
>> c = gauss + 'signal = signal + zeros(size(x));';	% add code after the Expression (append)
>> c = 'disp(''Gaussian comming'');'+ gauss;		% add code before the Expression (prepend)
Last, when using a single word character string as one of the arguments to a binary operation, a constant Parameter is used, for instance :
>> c = gauss + 'Background'			% add a new Background parameter
>> c = gauss + constant('Background')		% same as above
>> c = gauss + constant				% same as above, but not naming explicitly the new Constant
>> d = gauss.*'Amplitude' + 'Background'	% add 2 new constant Parameters
You can also use the convolution related operators
In these methods, when one of the argument is scalar, a Gaussian function of that width is built for convolution/correlation.
>> a = convn(lorz, 3)		% convolution of a Lorentzian with a Gaussian of width 3
>> a = convn(lorz, gauss)	% a Voigt function...
>> a = convn(lorz, 'double(b)'); a.Constraint = 'global b';	% convolute with a global variable 'b'
Methods generally mimic the Matlab default ones in functionality, and are also similar to those of the iData objects (see the Methods page).

It is possible to apply binary operators on mixed type arguments (e.g. a Data set and a Model), in which case the result depends on the arguments, as detailed in the 'binary operators with mixed arguments' help.

Optimising the iFunc model parameters

It is possible to optimize the model parameter values in order to minimize or maximize the model value, with the 'fmin' method. For this, any optimizer can be used, e.g.
>> p = fmin(model)
will use some guessed axes and automatic optimizer choice for the optimisation. To start the optimization for a given initial parameter set, use:
>> p = fmin(model, starting_pars)
The starting parameters can be given as a vector, structure or string such as 'Intensity=1' as explained above.
When given as a structure or a string, the resulting optimised parameters are returned as a structure.

You may also set manually the optimizer configuration and axes to use with:
>> p = fmin(model, starting_pars, options, x,y, ...)
Just as detailed in the Optimizers documentation, you may specify the 'options' as the name of the optimizer (then using its default configuration), a string, or a structure, such as in the following examples:
>> p = fmin(model, starting_pars, 'fminpso')
>> p = fmin(model, starting_pars, 'optimizer=fminpso; OutputFcn=fminplot; Display=iter')
By default, the axes to use for the evaluation will be guessed. In order to explicitly specify the axes to use, add them after the options:
>> p = fmin(model, starting_pars, 'optimizer=fminpso; OutputFcn=fminplot; Display=iter', x,y, ...)
In all cases, it is strongly advised to fix the non-relevant parameters, and bound the others, as explained above.
For instance:
>> model= gauss1;
>> fix(model, 'all'); model.Intensity='free';
>> model.Intensity=1; model.HalfWidth=.5;
>> xlim(model, 'Intensity',[-2 2])
>> fmin(model)
ans =
   -2.0000         0    0.5000
>> fmin(model, 'Intensity=1')
ans = 
    Intensity: -2
will search for the intensity that minimizes a Gaussian. This is of course the lower Intensity bound, other parameters being fixed.

It is also possible to maximize the model parameters with the similar 'fmax' method. The result is then the upper Intensity bound.
>> model= gauss1;
>> fix(model, 'all'); model.Intensity='free';
>> model.Intensity=1; model.HalfWidth=.5;
>> xlim(model, 'Intensity',[-2 2])
>> fmax(model)
ans =
    1.9995         0    0.5000

Fitting model parameters onto data

NOTE: a more detailed documentation on this topic is available in the Fit page.

Once models have been assembled, it is possible to use them for fitting, that is find the best parameter values to match a data set. The syntax for this is :
>> p = fits(model, data, starting_parameters, options, constraints, ...)
The data can be given as an iData object, a vector/matrix,
data=[ .... ]
a structure with members
data.Signal
data.Error
data.Monitor
data.Axes={x,y,...}
or a cell
data={ x,y, ... , Signal }

Similarly to the iData objects, the 'x' 1st rank axis corresponds to rows, 'y' to columns. When the data has a higher dimensionality as the model, this latter is extended by orthogonal multiplication to match the data dimensionality. It is thus possible for instance to fit a 4D data set with the default 'gauss' model, which then results in the creation of the 'gauss*gauss*gauss*gauss' model.

The fit begins from the given starting values, or from guessed values if entered as empty. Other options and constraints, as well as returned arguments, are the same as described in the Fit page. Empty input argument values request the fit to use default values.
	>> data=load(iData, [ ifitpath 'Data/sv1850.scn' ])
	>> p=fits(data);	% fit to a gaussian
or with a specific optmiser choice:
	>> [p,c,m,o]=fits(gauss,data,[],'optimizer=fminpowell; OutputFcn=fminplot');
The model value when the fit procedure ends is stored in the output.modelValue member :
>> [parameters,criteria,message,output]= fits(model, data, initial_parameters,...)
which is an iData object when data is given as an iData. In this case, fits(iFunc, iData, ...) is equivalent to fits(iData, iFunc, ...), and you can directly plot the result on top of the initial data with:
>> plot(data, output.modelValue)
When the data to be fitted is not an iData object, you can plot the fit result from e.g.
>> plot(output.modelAxes,output.modelValue)	% 1D
>> surf(output.modelAxes{:},output.modelValue)	% 2D

E. Farhi - iFit/iFunc objects - Nov. 27, 2018 $Revision:1.7 $ - back to Main iFit Page ILL, Grenoble, France <www.ill.eu>